The living universe is made of cognitive energy that inherently contains a pattern of information which makes it capable of organizing itself into self-organizing nonlinear networks. I propose that the fractal dimension of the Golden Ratio could contain this pattern of information; therefore, I will briefly explain fractal geometry and the golden ratio.
Fractal geometry is the geometry of chaos. If we take a nonlinear function and assume initial values for constants and variables for the first round of iteration, on each round we will get a value that we will feed back into the system. Now, if we analyze the values that we obtained at each iteration, we may see patterns where the values are diverging, converging, or constant. Then we reach a zone where the results provide chaotic values without any traceable pattern. With the help of a computer, we can divide the chaotic zone into much smaller increments and plot the values.
The result of this plot reveals self-similar patterns in which any magnified part looks just like the larger section from which it was taken. Even though we see chaos on the surface, at deeper levels we observe that the elements are creating an emerging order of self-similar patterns, where in different scales they display the same degree of order. The most surprising quality of fractals is that they are created by repeating basic operational rules which signifies a deep simplicity at the core of this complex universe.
Fractal mathematics is geometry of the real world, which has rough or irregular surfaces. In contrast, Euclidian geometry is based on the assumption that surfaces are smooth (planes have only two dimensions). Euclidian geometry assumes that structures exist only in whole dimensions (1, 2, 3), but fractal geometry allows us to explain the fractional dimensions that exist in the real world (e.g., a snowflake’s dimension is 4/3). Fractal geometry describes chaotic transition. Fractal mathematics is one of the greatest achievements of the human mind in the digital age.
Golden ratio (phi):
The golden ratio is the most irrational number (in up to 20,000 decimals, there is no trace of repeating patterns), but it creates beauty and order in art and natural world phenomena.
Mario Livio’s book, ”The Golden Ratio: PHI, the world’s most amazing number,” explains the role of phi in human history. In it, Livio says that Euclid first described phi more than 2,000 years ago. In the natural world, it appears in mollusk shells, sunflower florets, crystals, and galaxies. As a critical concept in mathematics and physics, it made possible the construction of pentagrams, the Egyptian pyramids, and the Roman Parthenon. Phi is featured in poetry, music, and great works of visual art, such as Leonardo da Vinci’s “Mona Lisa” and Salvador Dali’s “The Sacrament of the Last Supper.” Some psychologists believe the golden ratio is the most aesthetically pleasing proportion to the human mind, and followers of Pythagoras believed it revealed the hand of God.
In the 1930s, the accountant Ralph Nelson Elliott published his “wave principle,” which suggested that the golden ratio is connected to the behavior of the stock market. According to Gregg Braden in his book Fractal Time, “The golden ratio applies to everything from the brain’s states of consciousness to the proportions of DNA itself. For example, one complete turn of a DNA strand is 34 (angstrom units) in length and 21 wide. Each of these lengths is a member of the Fibonacci sequence,” which their ratio represents the golden ratio.
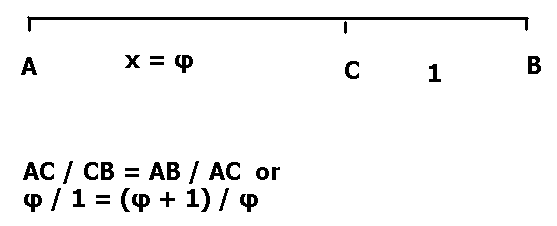
The universality of the golden ratio provides all kinds of self-similar algebraic forms and geometric shapes. If we choose point C on a one-dimensional segment of AB, such that the proportionality of the larger AC over the smaller CB is equal to the proportionality of the whole AB to the larger AC, the product is the golden ratio.
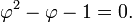
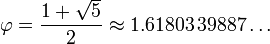
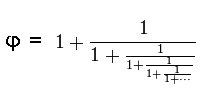
In two dimensions, if we create a rectangle where phi = a/b, a = length, and b = width, this rectangle is called the golden rectangle. Amazingly, if we take away one square from this golden rectangle, the remainder is also a golden rectangle. This process could continue indefinitely, and each time we’d end up with smaller but self-similar golden rectangles. Also, if we connect similar points in these golden rectangles, we end up with a spiral pattern called the golden spiral.
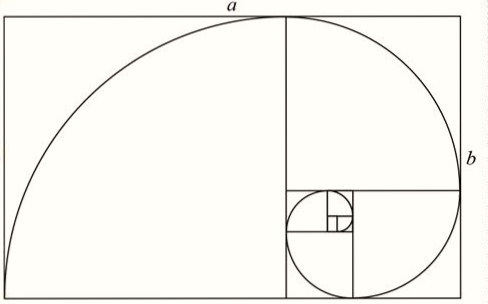
In three dimensions, if we create a golden cube and take away smaller cubes, we again end up with never-ending, self-similar but smaller golden cubes. And again, by connecting the self-similar points in these golden cubes, we end up with the golden spiral, which creates these self-similar shapes in three-dimensional spaces.
Therefore, the golden ratio, through its spiral patterns, creates self-similarity in Euclidian geometry.
Nonlinear Mathematics are mathematic of patterns and process in chaotic zone; fractal geometry is the proper geometry of self-organizing non-linear living networks. So if the golden ratio provides the self-similarity of shapes, through its spiral patterns, in Euclidian geometry, then, the fractal dimensions of the golden ratio will represent a spiral pattern which guides the universality of self-organizing process. It makes the living universe capable of organizing itself in nonlinear network patterns without any central command.
A recent study done by Steven Strogatz looked at the synchronization of networks in three dimensions. What he found supports the existence of spiral patterns within all networks excitations. Strogatz traced spiral patterns in chemical “BZ” reactions that rhythmically alter between sky blue and rusty red dozens of times. These reactions are named for their discoverers, Boris Belousov and Anatol Zhabotinsky.
As Strogatz writes in his fascinating book Sync: The emerging science of spontaneous order, “Spiral waves are now recognized to be a pervasive feature of all chemical, biological, and physical excitable media…. The most striking thing about spiral waves is that they seem to be alive (emphasis mine). They are self-sustaining, they don’t need pacemakers”. “If you watch one in a thin layer of excitable BZ reaction, it looks like a perpetual pinwheel, chasing its tail and regenerating itself endlessly.”